“data”: sequence alignment

A sequence alignment is not a fact

… it is a complex inference.

In molecular phylogenetics, homology means…

In molecular phylogenetics, homology means…

Thus sequence alignment for phylogenetics is
a super challenging inference. More about this later.

Types of phylogenetic inference methods

• Distance-based
• Parsimony
• Likelihood-based
  • Maximum likelihood
  • Bayesian

Distance-based phylogenetics

Distance-based phylogenetics

Note that the matrix doesn’t have to come from sequence data.

Parsimony phylogenetics

Parsimony is based on Occam’s razor

Among competing hypotheses that predict equally well, the one with the fewest assumptions should be selected.

Say we have three viruses

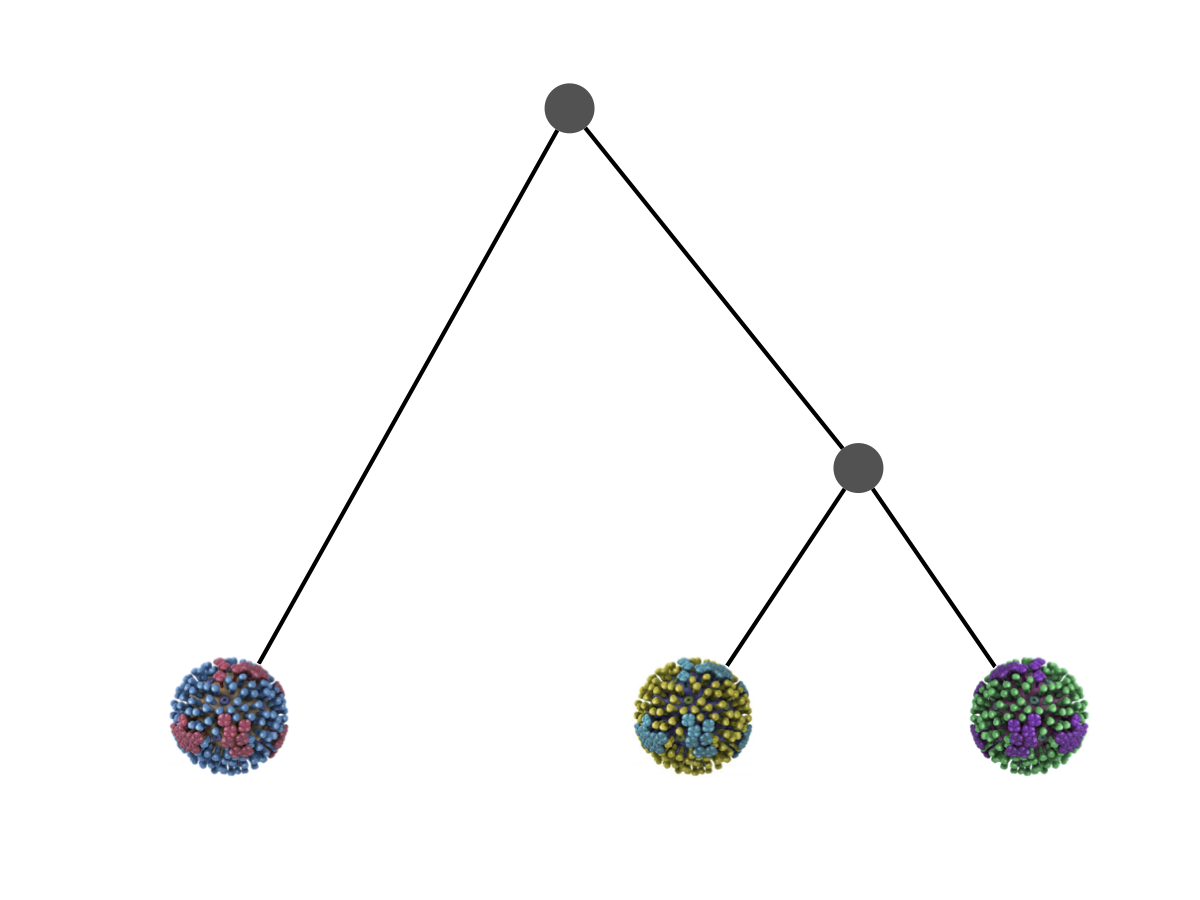
Say we have three viruses

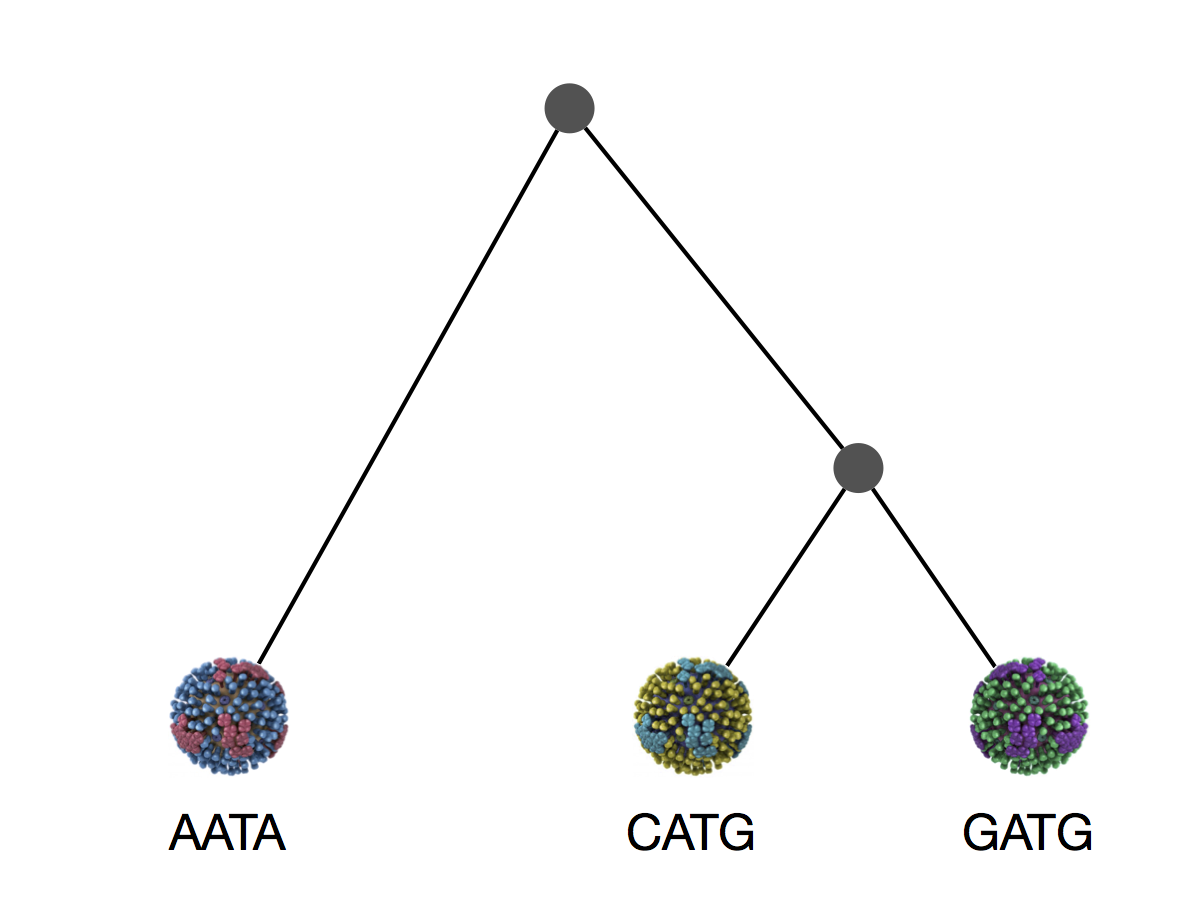
We can explain these sequences with 3 mutations

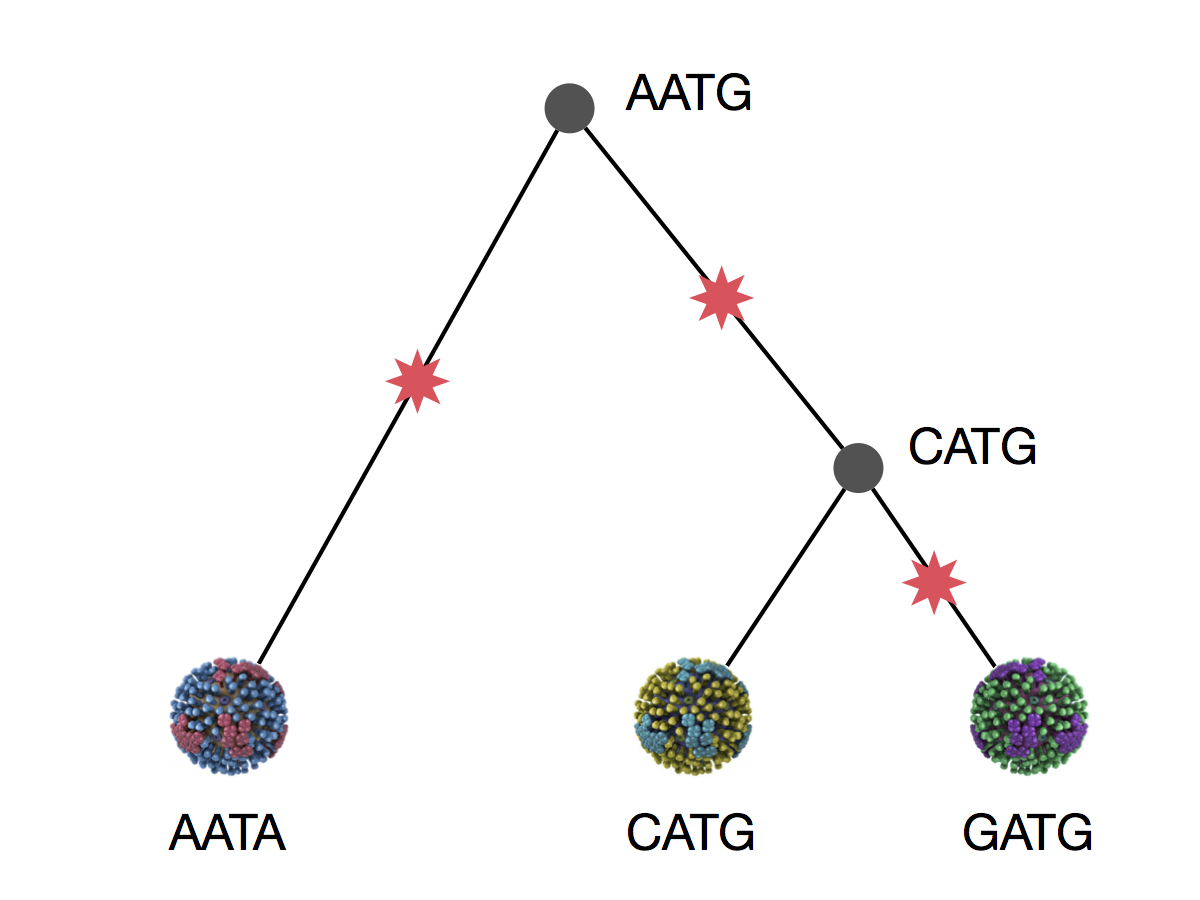
This topology requires 3 mutations at minimum

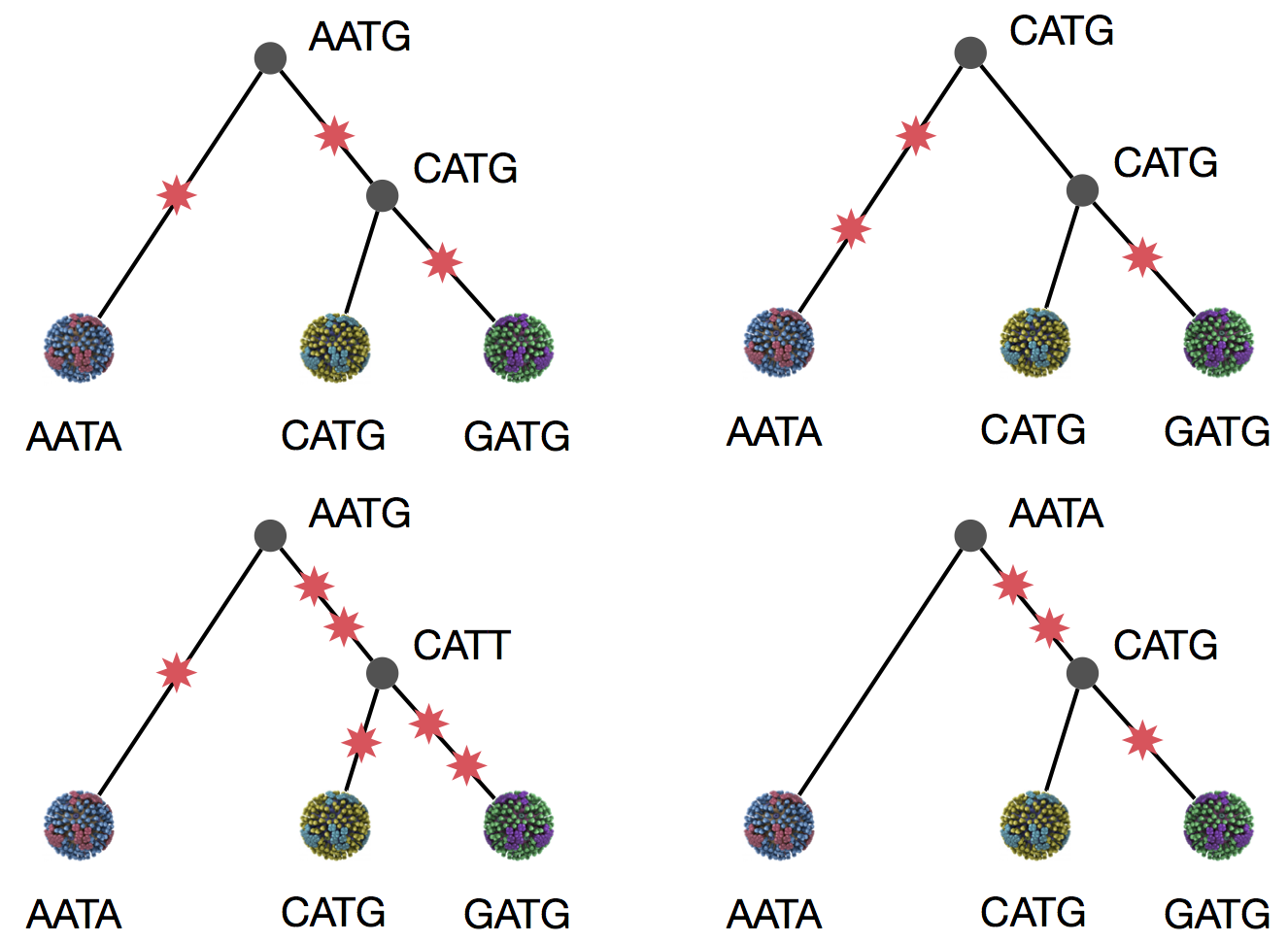
Exercise: which topology is more parsimonious?

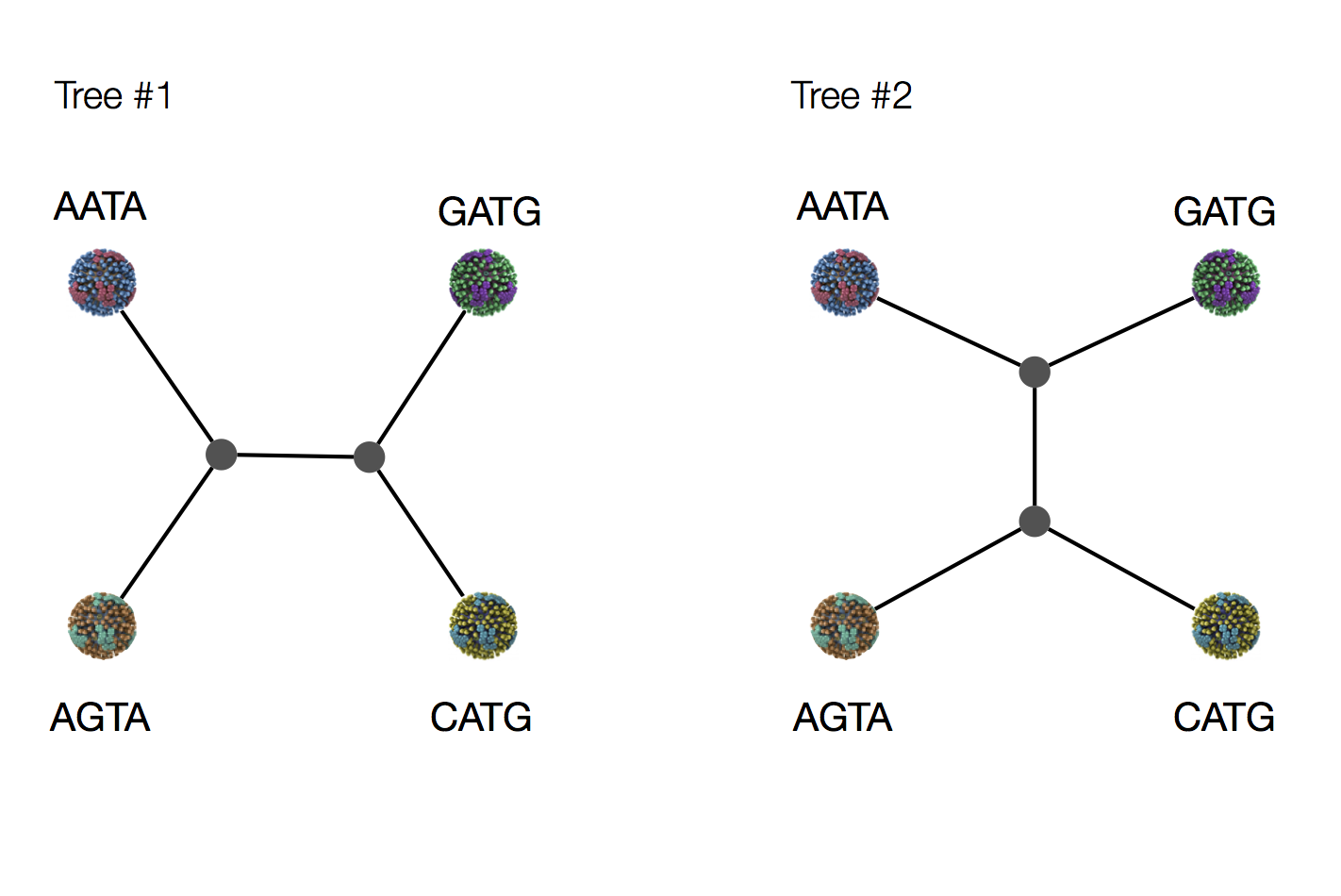
Exercise: which topology is more parsimonious?

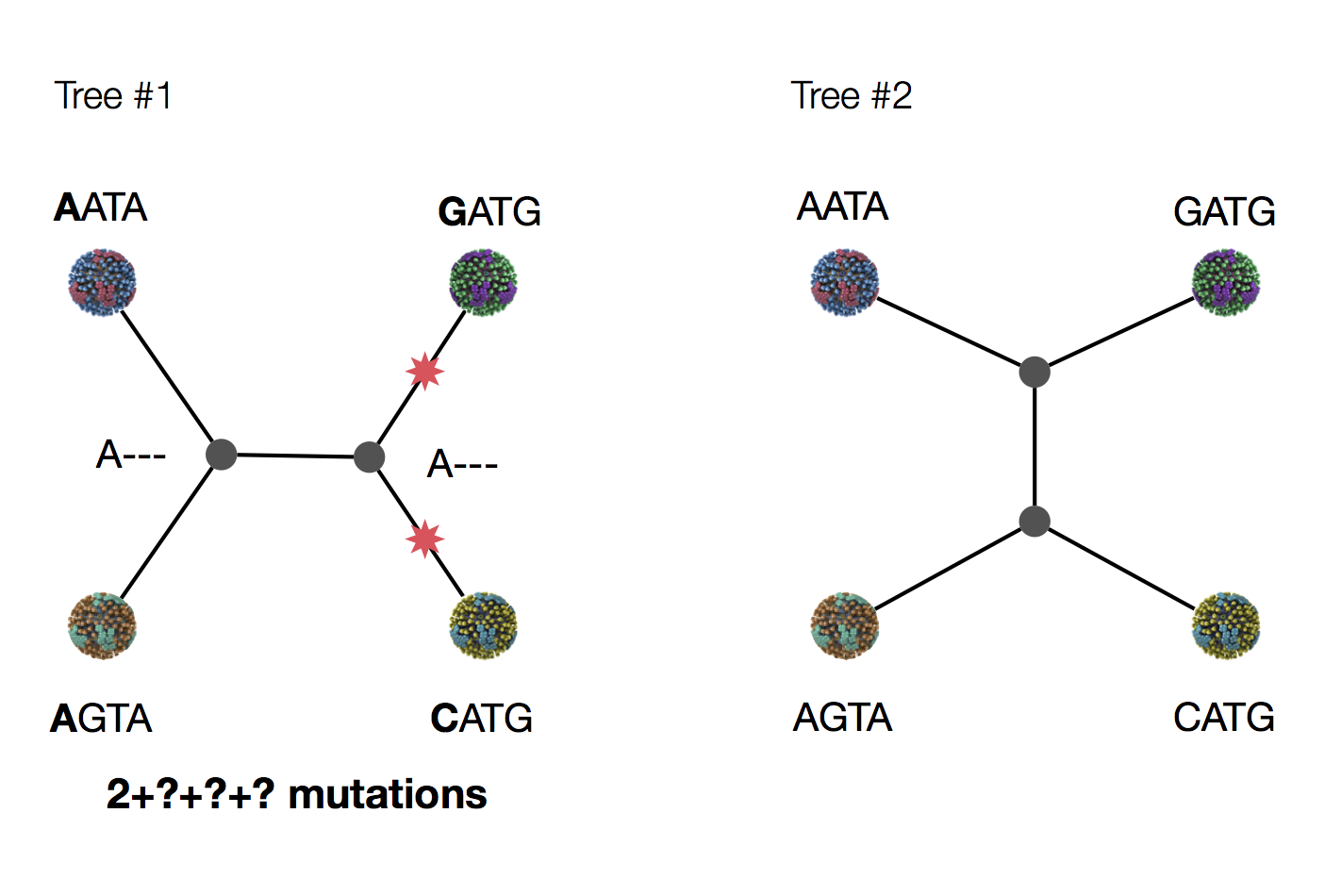
Exercise: which topology is more parsimonious?

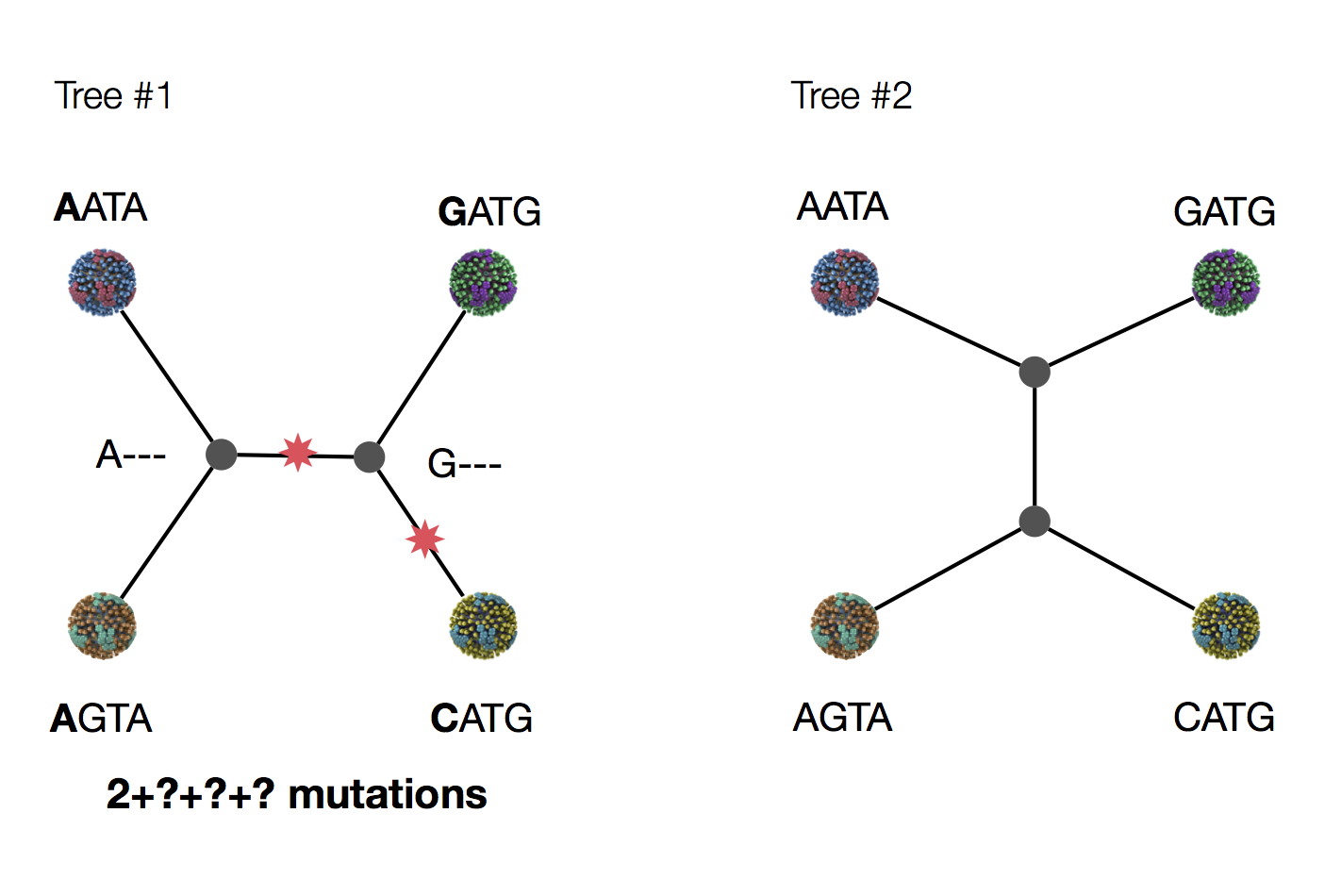
Exercise: which topology is more parsimonious?

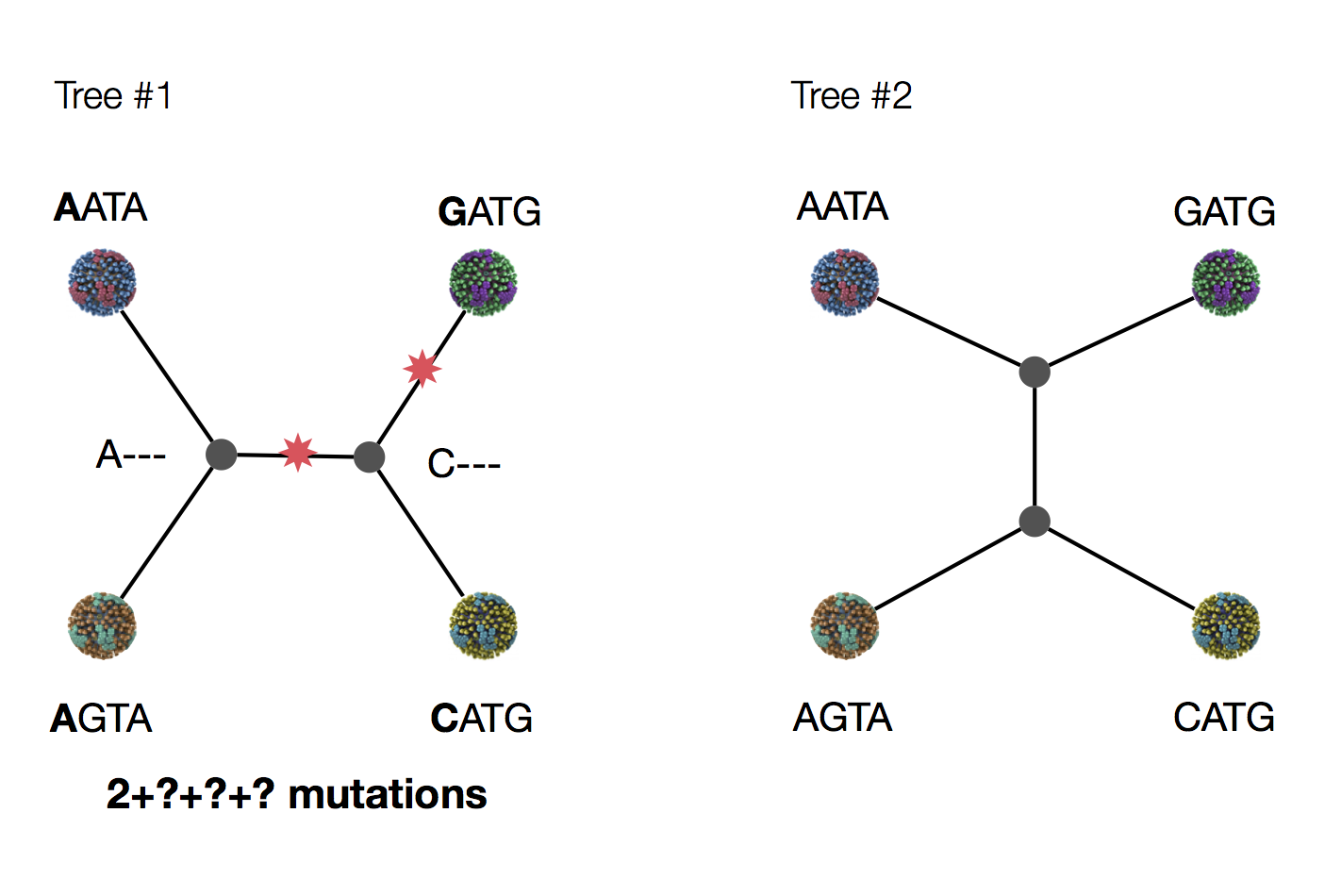
Exercise: which topology is more parsimonious?

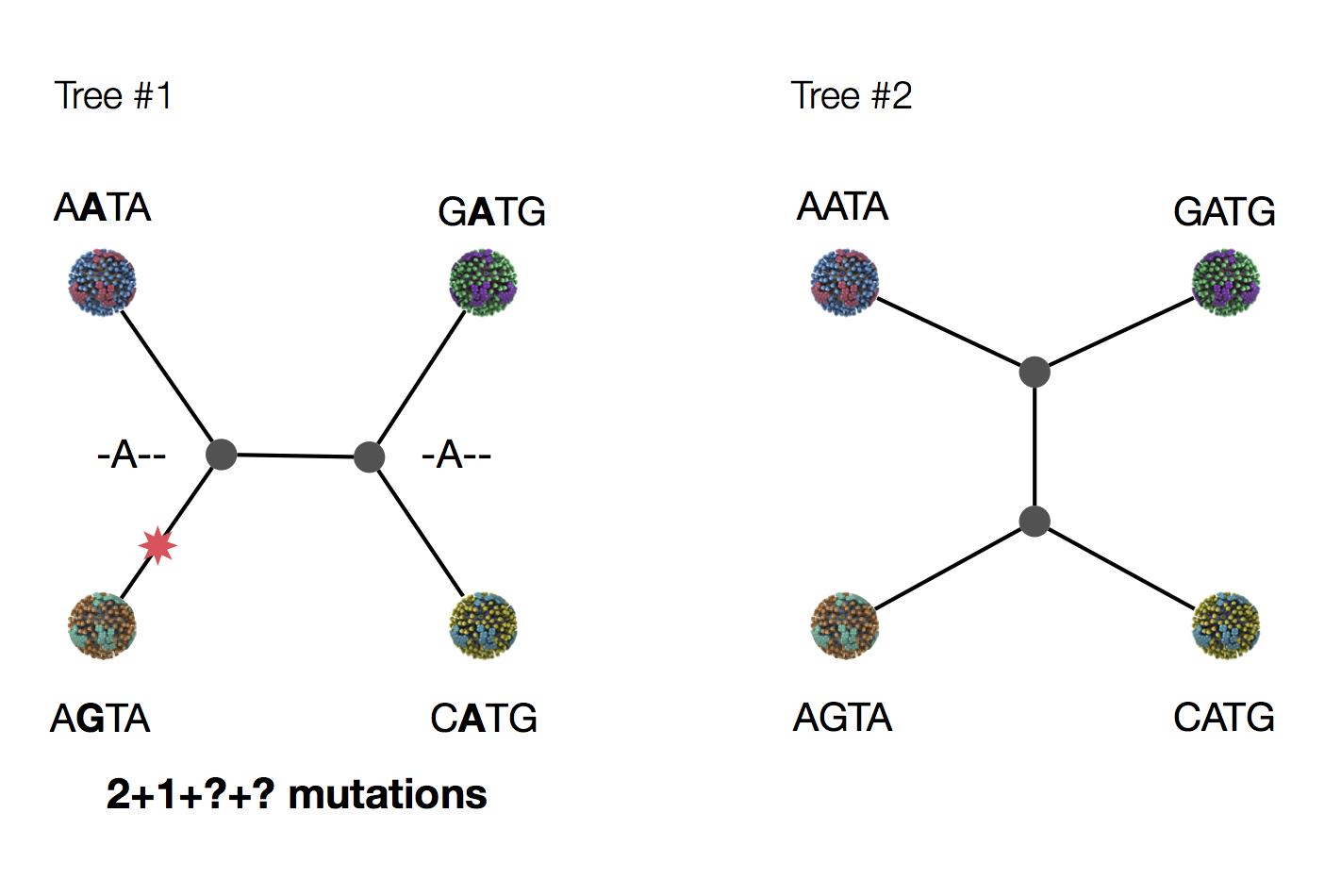
Exercise: which topology is more parsimonious?

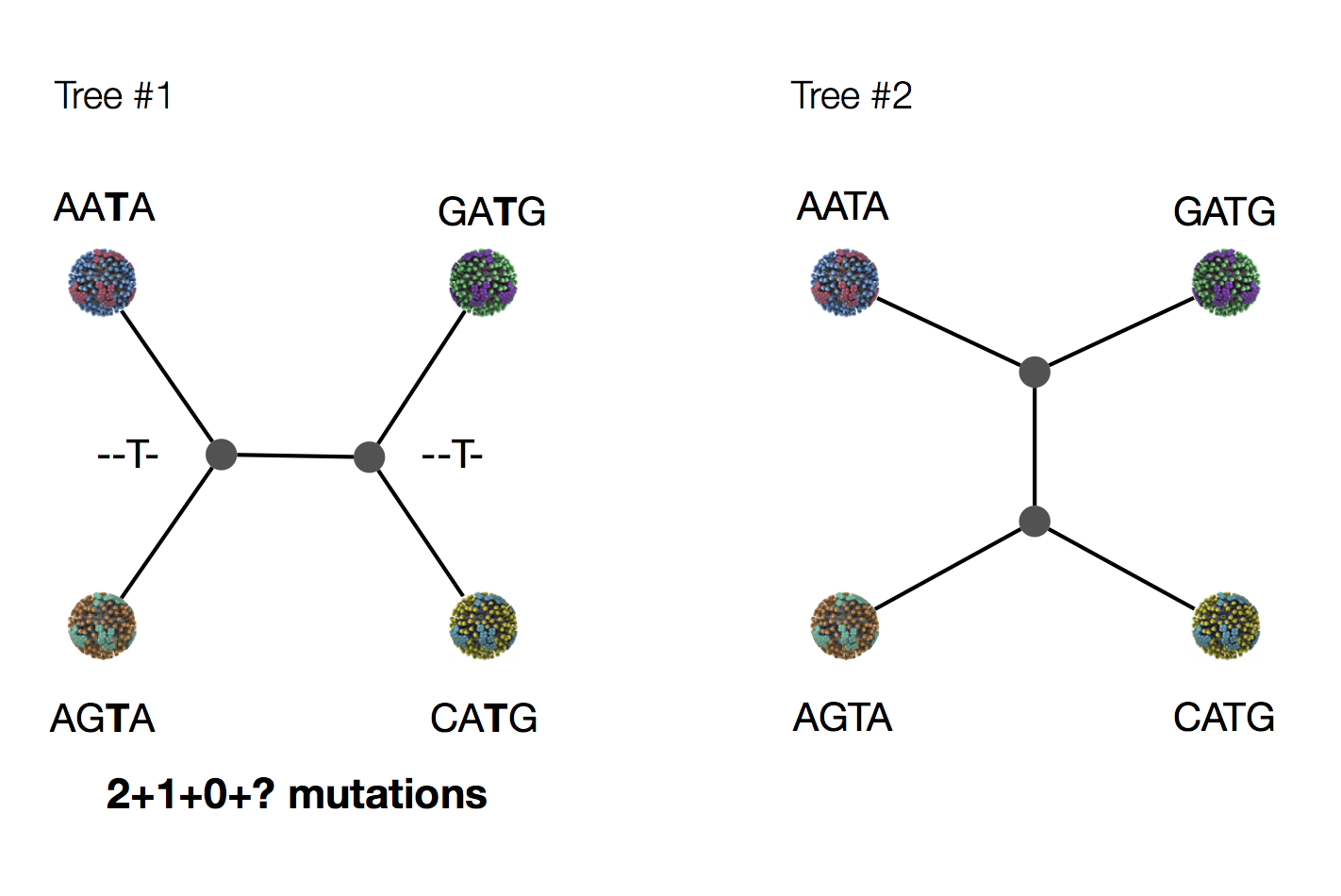
Exercise: which topology is more parsimonious?

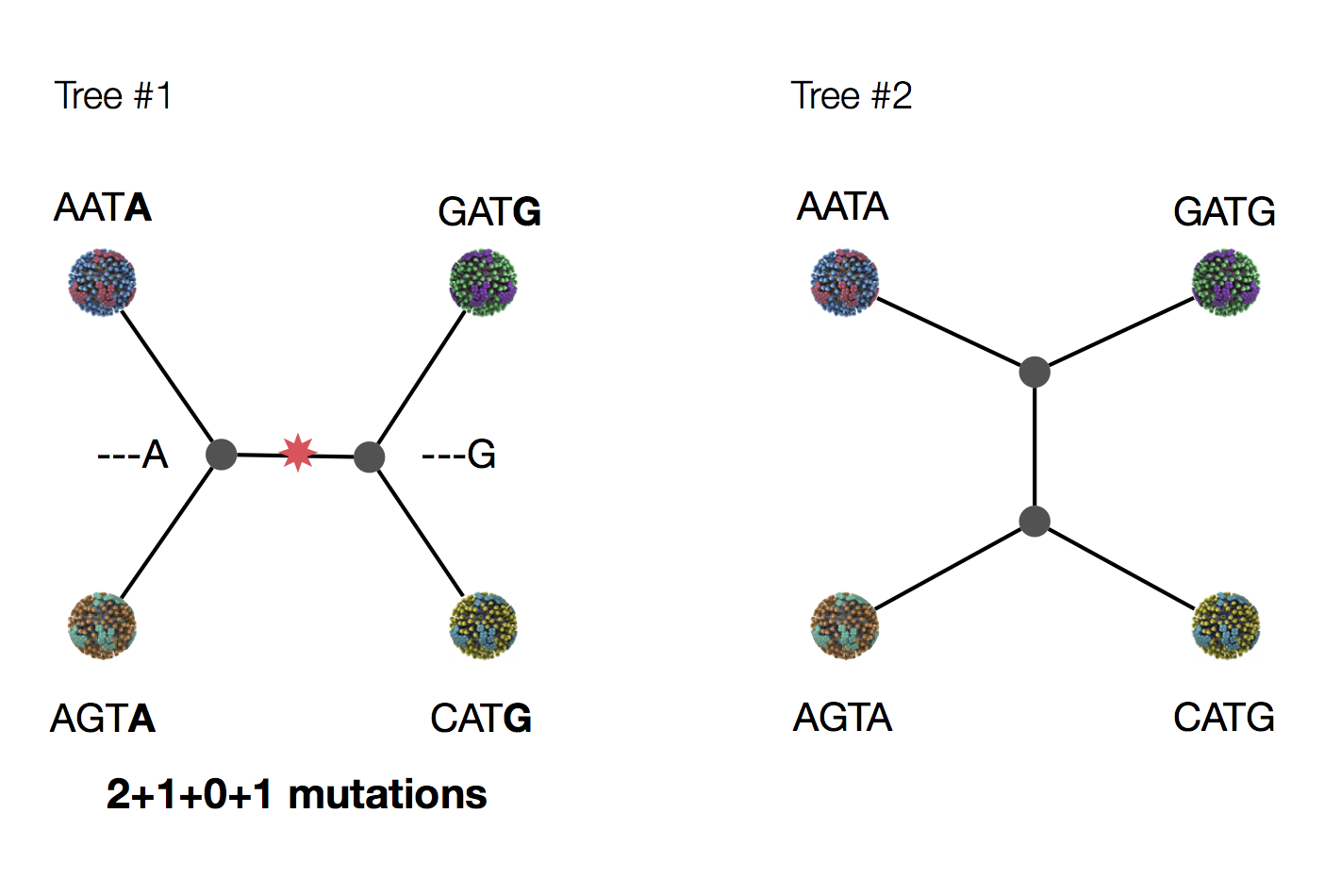
Exercise: which topology is more parsimonious?

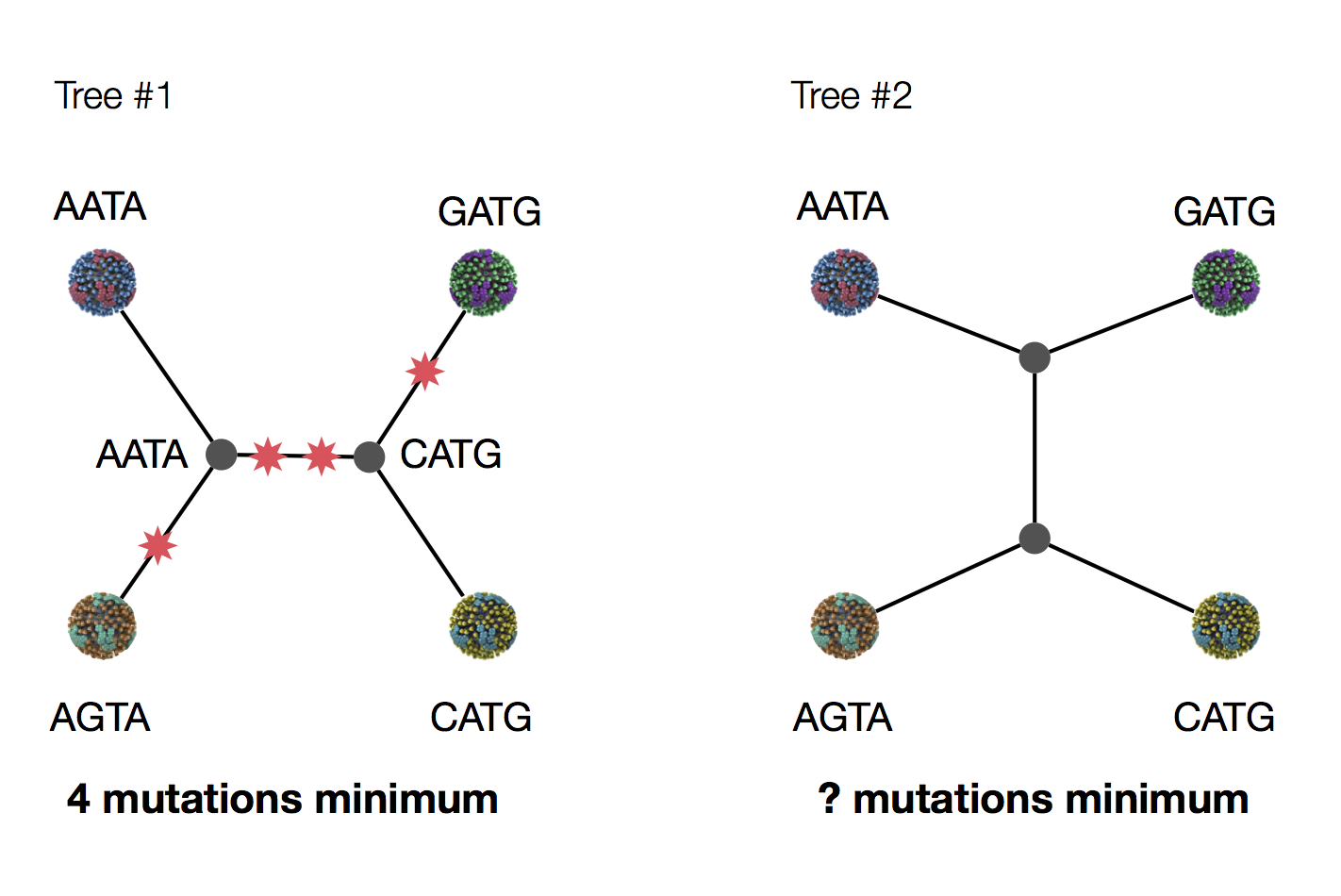
Parsimony seems sensible.

Is it the most popular phylogenetics method?

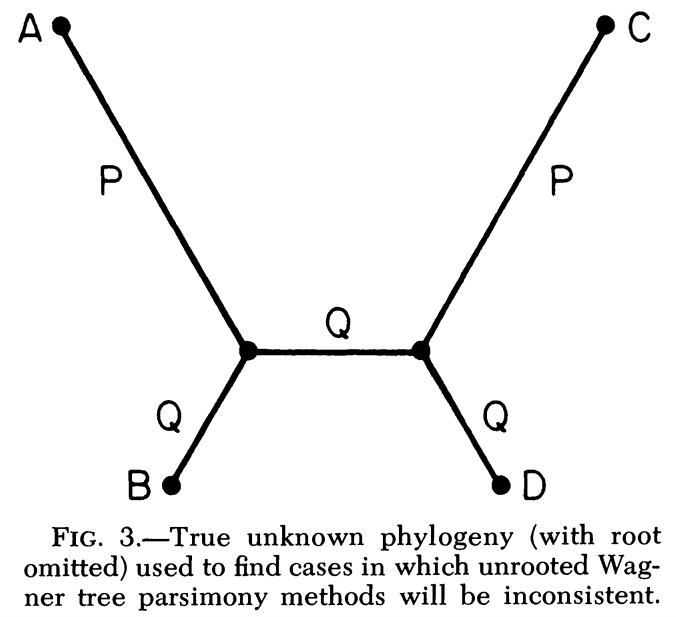
Long branch attraction

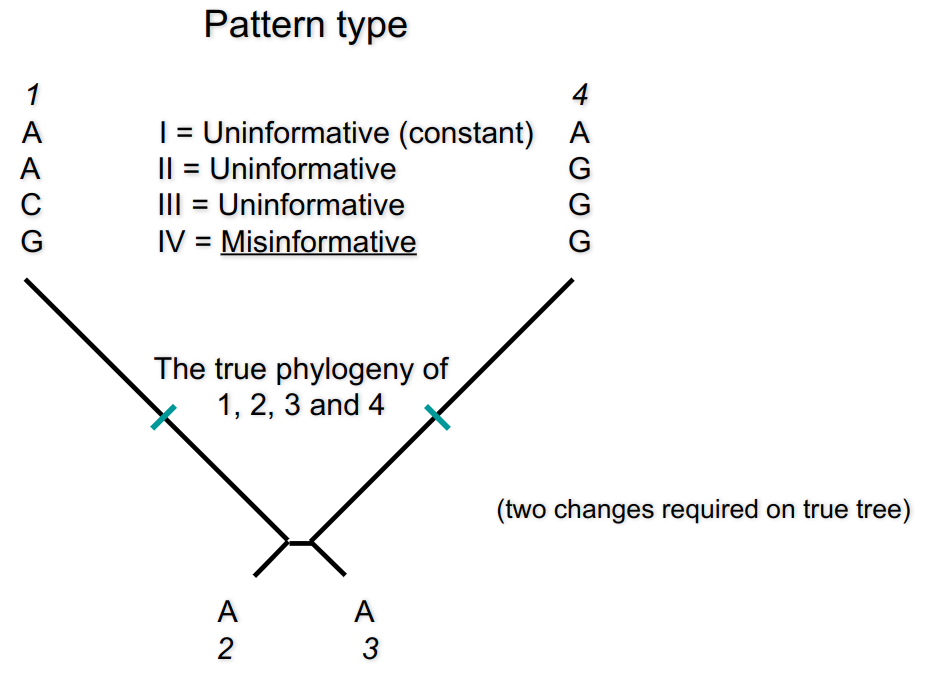
Long branch attraction

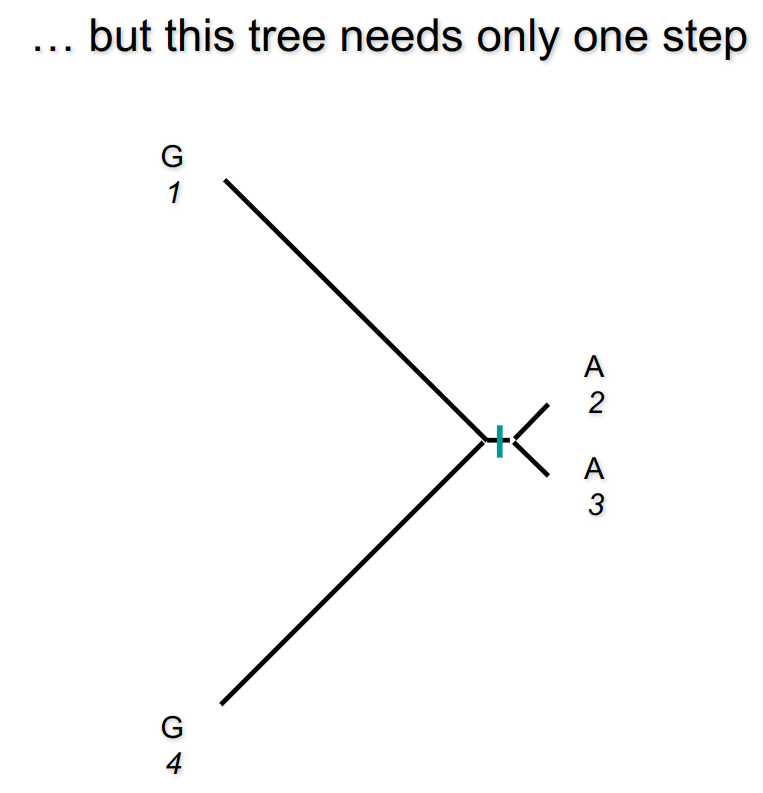
Are we cooked?

Likelihood setup

• Come up with a statistical model of experiment in terms of some data and some parameters
• Write down a likelihood function that expresses the probability of generating the observed data given those parameters
• Now we can evaluate likelihood under various parameter values
• We will write this likelihood \(\Pr(D \mid \theta)\).
  Why is this appropriate notation?

Example: picking peaches

Say \(p\) is the probability of getting a ripe peach, and each draw is independent.

• What is the probability of getting two ripe peaches in a row?
• What about if after harvesting two peaches, we have one ripe one?
• What about if after harvesting 20 peaches, we have 6 ripe ones?

Example: picking peaches

Say that, after harvesting 20 peaches, we have 6 ripe ones.

Say \(p\) is the probability of getting a ripe peach, and each draw is independent. Model using the binomial distribution.

The likelihood of getting the observed result is \[ { {20} \choose 6} \, p^6 \, (1-p)^{20-6}. \] Recall: \({ {20} \choose 6}\) is the number of ways of choosing 6 items out of 20.

Peach picking likelihood surface

The maximum likelihood estimate of the parameter(s) of interest is the parameter value(s) that maximize the likelihood.

Questions

1. What is the maximum likelihood (ML) estimate of \(p\) given our experiment?
2. Would the result of this ML estimate be different if we got 60 ripe peaches out of 200?
3. Intuitively, would the shape of the likelihood curve be different with this larger dataset?

Likelihood recap

• Maximum likelihood is a way of inferring unknown parameters
• To apply likelihood, we need a model of the system under investigation
• In general, the “likelihood” is the likelihood of generating the data under the given parameters, written \(P(D | \theta),\) where \(D\) is the data and \(\theta\) are the parameters.

Crazy but typical model assumptions

• differences between sequences only appear by point mutation
• evolution happens on each column independently
• sequences are evolving according to reversible models (this excludes selection and directional evolution of base composition)
• the evolutionary process is identical on all branches of the tree