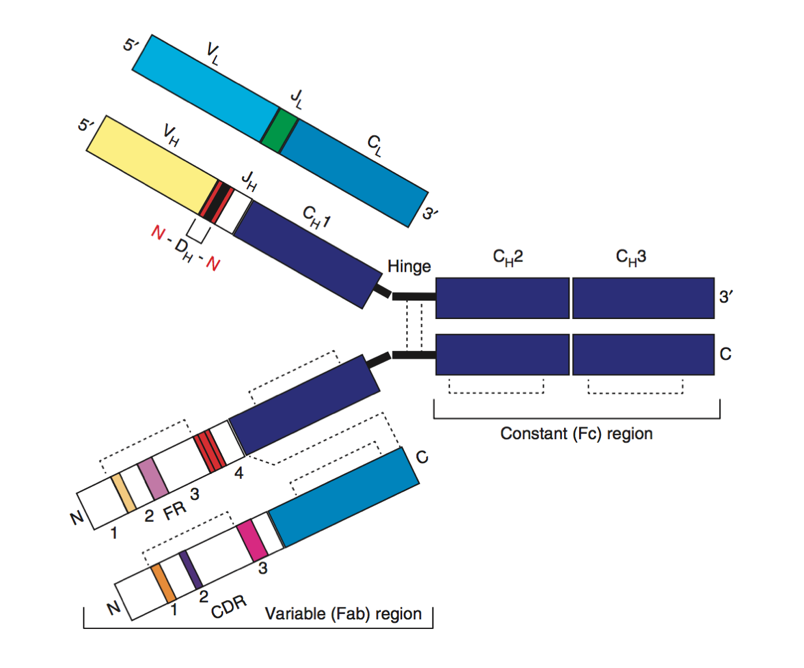
Structure of a B cell receptor

VDJ recombination

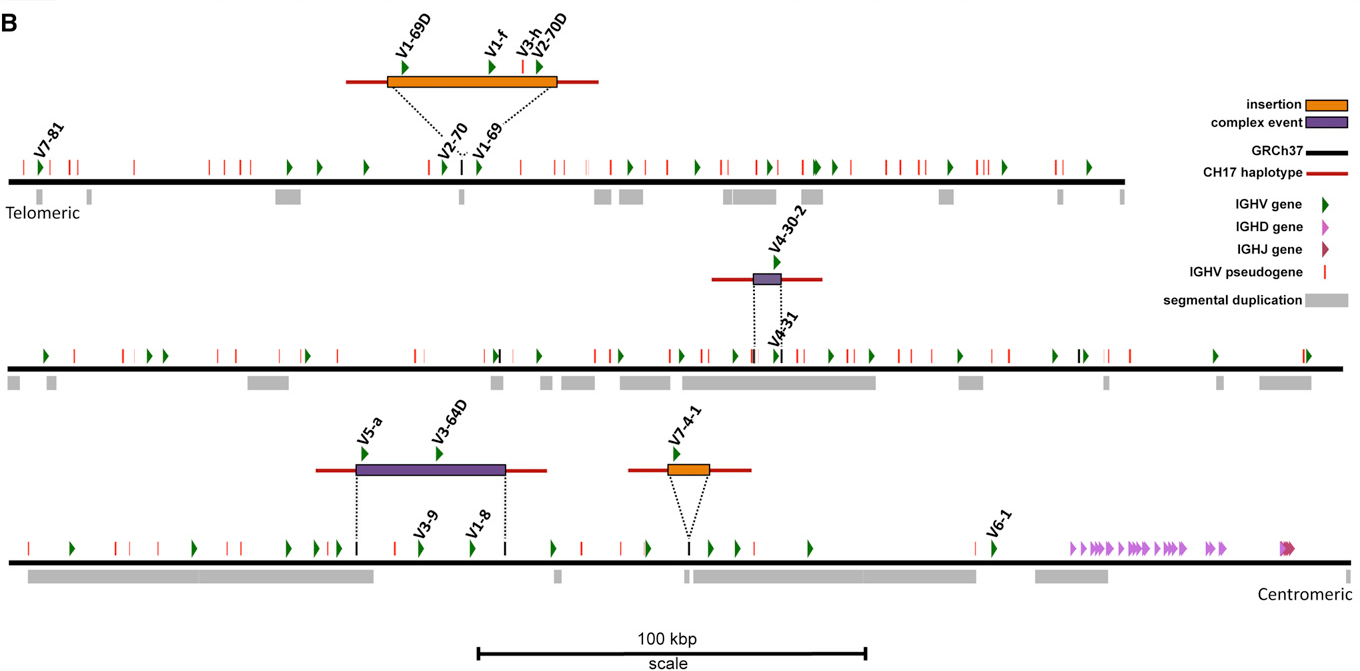
VDJ loci

Somatic hypermutation is AID + repair

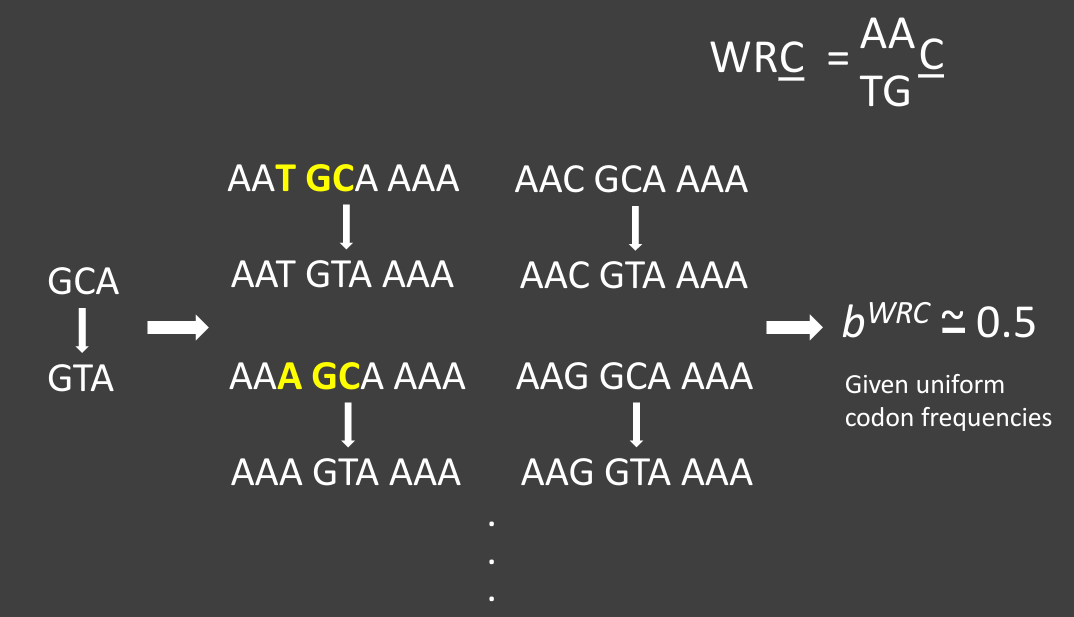
The mutations have peculiar biases

The mutations have peculiar biases

Phylogenetics is not straightforward

Incorporating context sensitivity helps performance

What about natural selection?

Remember goal: get per-site selection inferences,

• \(\omega > 1\) indicates positive selection (“invites change”)
• \(\omega < 1\) indicates negative selection (“does not tolerate change”)

Natural selection inferences are also not straightforward

Natural selection inferences are also not straightforward

Natural selection inferences are also not straightforward

Context-sensitive mutation can confound
natural selection inference for B cells.

Correct for mutation rate variation

• \(\lambda_l^{(N-I)}\): nonsynonymous in-frame rate for site \(l\)
• \(\lambda_l^{(N-N)}\): nonsynonymous neutral rate for site \(l\)
• \(\lambda_l^{(S-I)}\): synonymous in-frame rate for site \(l\)
• \(\lambda_l^{(S-N)}\): synonymous neutral rate for site \(l\)

\[ \omega_l = \frac{\lambda_l^{(N-I)} / \lambda_l^{(N-N)}}{\lambda_l^{(S-I)} / \lambda_l^{(S-N)}} \]

How do we get neutral per-site substitution rate?

Productive vs. out-of-frame receptors

Out-of-frame reads can be used to infer neutral mutation rate.

One can also use passenger alleles

• Yeap, Hwang, Du, Meyers, …, Alt, F. W. Cell, 2015
• Cui, Di Niro, Vander Heiden, Briggs, … , Kleinstein J Immunol, 2016.

and fit a mutation model.

One would like to quantify these biases

Classic work by Kleinstein group

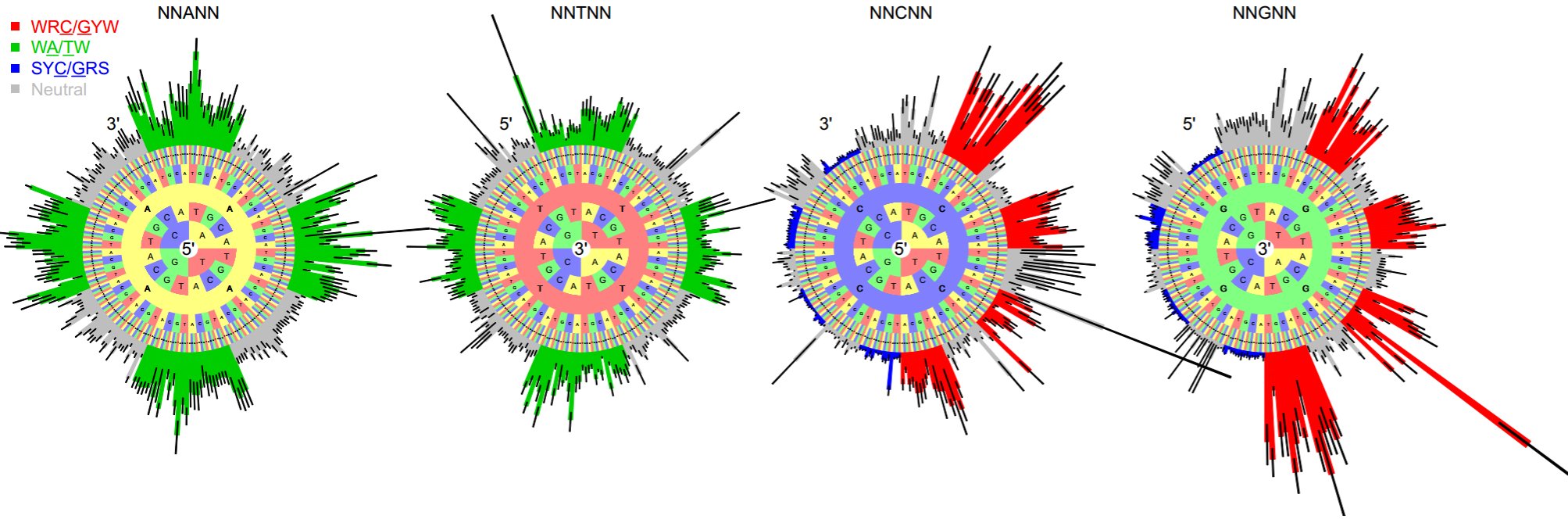
• Yaari, Vander Heiden, Uduman, Gadala-Maria, Gupta, Stern, Kleinstein, Front Immunol, 2013.
• Cui, Di Niro, Vander Heiden, Briggs, … , Kleinstein J Immunol, 2016.

Have extended this framework

We can add overlapping motifs.

Feng, Shaw, Minin, Simon, & M, arXiv, in revision for Ann. Applied Stat.

Inferring natural selection

• BASELINe infers overall selection: Yaari, Uduman, Kleinstein Nucleic Acids Research, 2012 [DOI]
• Infer whole-repertoire per-base selection: McCoy, Bedford, M Phil. Trans. Royal Soc. London, 2015 [DOI]
• IgPhyML infers selection in a phylogenetic context: Hoehn, Lunter, & Pybus Genetics, 2017. [DOI]

It’s not all bad news!

Motivation

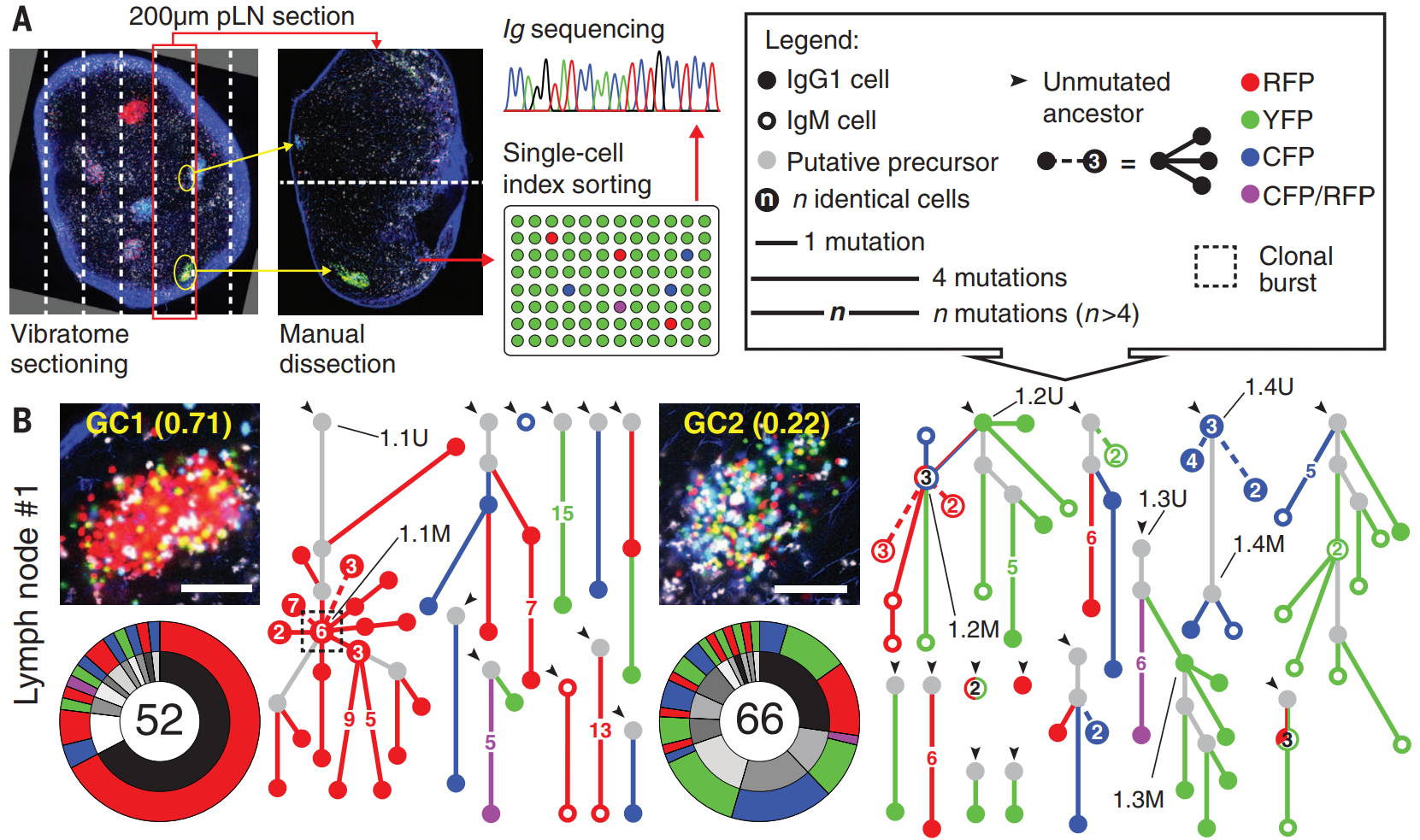
Goal:

Accurate tree inference using not-very-diverged sequences
which are sampled with meaningful counts

A simple infinite-type branching process model

• \(p\): probability of division
• \(q\): probability of mutation

“GCTree” likelihood

Incorporating model likelihood

• Given sequence data, construct maximum parsimony trees
  (there are lots, typically)
• Pick the tree with the highest model likelihood

GCtree works in simulation

GCtree finds more common IgH and IgL trees